使用A*算法解决路径寻找问题,并回答几个问题。
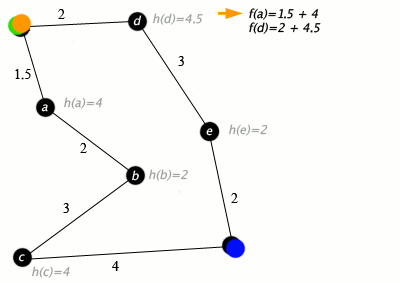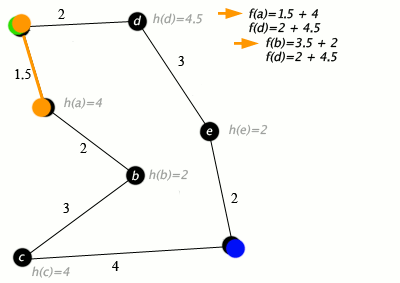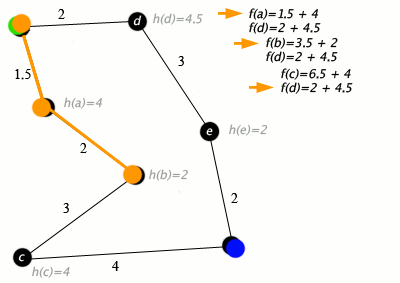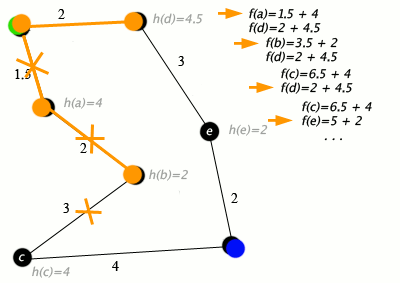
Question-1: Problem Solving as Search
The Problem
Consider a grid of size N x N that represents a topographic map. Each tile describes the characteristics of its terrain, which could be of two types: normal or mountainous. ROBBIE the robot must navigate from a starting position (xs,ys) to a goal position (xg,yg) using a learned algorithms (there can only be one start and one goal).
Note: In the explanations below, we assume that tile (1,1) is the top-left tile in the map.
Transition rules
ROBBIE is allowed to go to one of the (at most) eight surrounding tiles, as shown in Figure 1(a). However, it cannot move to a mountainous tile, and it cannot move diagonally if one of the directions composing the diagonal contains a mountainous tile. For instance, the black tile in Figure 1(b) represents a mountain, hence ROBBIE can move only to the five white tiles indicated by the arrows. In contrast, ROBBIE can move to seven tiles in Figure 1(c).
Path cost
ROBBIE’s wheels are built so that a diagonal move is the easiest. Hence, the cost of such a move is 1. Any other move has a cost of 2.
The Task
Your task is to write a Python 3 program called planpath that plans a path from a given starting tile to a goal tile.
- You should implement either Graph or Treesearch procedure to perform A*.
- Propose and implement a heuristic function for solving this problem.
- Determine whether this function is admissible or monotonic, and explain why.
Is the resulting algorithm A or A*?
- You will need to implement tie-breaking rules when all options have equal merit. Specify clearly in your documentation what are your tie-breaking rules.
Calling your program
Your program will have two command line arguments as follows:
python planpath.py INPUT/inputi.txt OUTPUT/outputi.txt Flag
Flag where the folders INPUT and OUTPUT should reside in the same folder as your program.
- inputi.txt - the name of the input file, where i is the number of the input file;
- outputi.txt - the name of the output file, where i is the number of the output file;
- Flag - indicates how many node expansions require a diagnostic output (if it is 0, no diagnostic output is required) - see the example later on in the assignment.
Input
- The first line will contain one number that specifies the number of rows and columns in the map.
- Subsequent lines will contain the map, one line per row. The following values will be accepted for each tile:
The following illustrates a procedure call and sample input for applying A/A* to a 3x3 map and printing diagnostic output for 5 iterations:
python planpath.py INPUT/input1.txt OUTPUT/output1.txt 5
where input1.txt is
3
SXR
RRR
XXG
Output
Your program should produce a sequence of moves that ROBBIE should perform to get from the start node to the goal, and the accumulated cost and ROBBIE’s position after each move.
Output format
- The sequence of moves should be formatted as a list of actions separated by dashes followed by a blank space and the cost of the path according to the algorithm. If no path was found, the output should state NO-PATH.
- The actions (in UPPER CASE) are: R (Right), RD (Diagonal Right-Down), D (Down), LD (Diagonal Left-Down), L (Left), LU (Diagonal Left-Up), U (Up), RU (Diagonal Right-Up).
- For example, a path that goes Start, Right, Right-Down, Down, Down, Left- Down and Goal, with a total cost of 8, is represented as follows: S-R-RD-D-D- LD-G 8
Programming Requirements
- Your program should be written in Python 3.
- Your program can only utilize Panads and Numpy package instead of any other advanced level packages.
- Your program should create a unique identifier for every generated node. The identifier of the start node should be N0, and other nodes should be identified as N1, N2, . . . according to the order in which they are generated. If you wish, you can include the actions used to reach a node in its identifier, e.g., N0-R-D. If you implement Graphsearch (as opposed to Treesearch), you need to identify when a repeated instance of a node is reached, and use only the first identifier created for this node.
- Your program should work on different maps, including those provided in moodle.
- The Graph/Treesearch procedure should build a search graph/tree respectively. Each node in the search graph/tree should have the following components:
- an identifier;
- the operator that generated it;
- order of expansion (if in CLOSED) otherwise 0;
- the cost g of reaching that node;
- a heuristic value h (0 for DLS);
- a value f, where f=g+h;
- a pointer to its children; and
- a pointer to its parent (if you implement Treesearch, and your action sequence is included in a node identifier, then this pointer is not necessary).
- In diagnostic mode (Flag 1), each time a node is expanded, your program should output the following components:
- node identifier;
- order of expansion;
- the cost g of reaching that node;
- a heuristic value h;
- a value f, wheref=g+h;
- the resolution of pointer to its children, i.e., the identifier of each child of the expanded node and the action that generated it;
- the lists OPEN (sorted in descending order of merit) and CLOSED. The value of Flag will be small, so don’t worry about OPEN and CLOSED being too long. Failure to print OPEN and CLOSED will result in loss of marks.
Output example
Say node N0:S at position (1, 1) is the first node to be expanded by some search algorithm not A*. The output for this step should be something like the following:
- N0:S 1 0 0 0 #ID expansion-order g,h,f
- Children: {N1:S-R, N2:S-RD, N3:S-D }
- OPEN: {(N1:S-R 2 0 2), (N2:S-RD 1 0 1), (N3:S-D 2 0 2)}
- CLOSED: {(N0:S 1 0 0 0)}
Question 2: First order logic, representation
Use the following vocabulary to express the assertions in the following sentences:
- MALE(x) means that the object denoted by x is male. - FEMALE(x) means that x is female.
- VEGETARIAN(x) means that x is a vegetarian.
- BUTCHER(x) means that x is a butcher.
- LIKES(x, y) means that x likes y.
- a. No man is both a butcher and a vegetarian.
- b. All men except butchers like vegetarians.
- c. The only vegetarian butchers are women.
- d. No man likes a woman who is a vegetarian.
Question 3: Unification
In the following pairs of expressions, w, x and y are variables, A and B are constants, and f and g are functions. Do these pairs of expressions unify? If they do, give the substitution that unifies them. If they don’t, then indicate where the unification fails.
- a. P(x,f(x),A,A)andP(y,f(A),y)
- b. P(x,f(x,y),g(x,w))andP(A,f(w,B),g(w,x))
Question 4: Resolution refutation
Consider the following statements:
- A student is successful if s/he has high grades.
- Students who are bright and work hard have high grades.
- Students who are not bright fail CSEXXX.
- Students who do not work hard have lots of fun.
- James is not having any fun.
- James passed CSEXXX
- a. Use the predicates SUCCESSFUL, HIGH-GRADES, BRIGHT, WORK-HARD, HAS-FUN and PASS (the opposite of FAIL) to represent these statements as predicate calculus formulas. DO NOT include STUDENT as a predicate, as it complicates the solution.
- b. Convert these statements to clauses.
- c. Use resolution refutation to prove that James is a successful student.
Question 5: Resolution refutation
Consider the following statements:
- Every boy or girl is a child.
- Every child gets a doll or a train or a lump of coal.
- No boy gets a doll.
- No child who is good gets a lump of coal.
- a. Use the predicates BOY, GIRL, CHILD, GET-DOLL, GET-TRAIN,GET-COAL and GOOD to represent these statements as predicate calculus formulas.
- b. Convert these statements to clauses.
- c. Use resolution refutation to prove that if no child gets a train, then no boy is good.