将提供的代码,使用MPI进行并行化处理,解决Navier Stokes Equation问题。
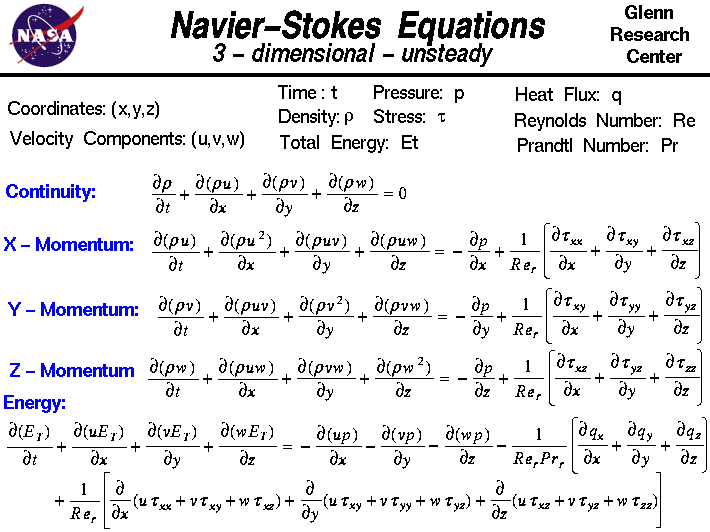
Theory and discretisation
In this coursework you will be solving the same set of equations that you did for the Modelling and Numerical Methods (MNM) coursework.
The governing equation
The aim of this assignment is to write a parallel solver for the NavierStokes equation. At each time step there will be an inner loop in which the pressure is solved using a projection method followed by an updating of the velocity.
Calculate an intermediate velocity.
Note that in order to calculate this divergence the values of the intermediate velocities on the boundaries of the domains will need to be communicated.
Once the divergence at each point has been calculated, the pressure Poisson equation can be solved iteratively using a Jacobi iteration.
Note that at every iteration the values of the pressure on the boundaries of the domain will need to be communicated.
Once the average residual is small enough these iterations can stop. Note that you will need to use a collective communication to find the average residual as it is not enough that it is small enough on a single process, but needs to be small enough across all processes.
Once the pressure has been found it can be used to update the velocities.
These updated velocities on the domain boundaries can now be exchanged with the neighbouring processors in order to allow the gradients in the intermediate velocity calculation to be obtained.
You can use a dynamic time step based on the Courant number (pre-factor in relationship between the time step and the ratio of the maximum velocity to the linear resolution), but be careful to ensure that there is a minimum time step to ensure that there aren’t issues at early time steps when the velocity is changing rapidly.
The domain, boundary and initial conditions - As a base case you are going to be solving the same problem that you had for the NMN coursework question 2 and part a. The fluid conditions and pressure drop should also be the same, namely water and you can use a default pressure drop 0.5 Pa.
The boundary conditions should be appropriate to each of the boundaries of the domain for both the pressure and the velocity (see NMN notes and the serial implementation).
MPI based implementation
You must use domain decomposition in which each processor only allocates enough memory to store its portion of the domain (together with any padding required to receive the data from neighbouring processes). The easiest way to divide the domain is into vertical or horizontal strips, but this can become inefficient quite rapidly as the number of processors grows as it will result in very long thin domains with a large number of boundary elements relative to their area. It is far more efficient to divide the simulation into rectangular domains that are as close to square as possible. The communication pattern involved is virtually identical to that implemented in Exercise 3 of worksheet 2 and will involve transferring a layer of grid cells just inside the edge of the domain from the neighbouring processors and receiving a layer of grid cells situated just outside the domain back from the neighbours. Note that you do not need to transfer data into the corners of the ghost layer around the edge of the domain as the finite difference stencil for all the equations used is a cross.
Your communications will take the form of peer-to-peer communications with no master process, with each process communicating only with its vertical and horizontal neighbours. Note that for a single time step there will be multiple sets of communications. The following overall calculation and communication strategy can be used:
- Calculate the size of the time step
- Collectively communicate the appropriate (minimum) time step
- Calculate the intermediate velocities (see equation 1 and serial code)
- Transfer domain boundary intermediate velocities to neighbours
- Calculate the RHS of the pressure Poisson equation (see equation 2 and serial code)
- Do one iteration of the Jacobi solver for the pressure Poisson equation (see equation 2 and serial code)
- Impose Neumann boundary conditions on any relevant boundaries if they are present within the current domain (see NMN note/serial implementation)
- Transfer domain boundary pressures to neighbours
- Collectively communicate the residual
- Repeat from step 6 if residual is still too large
- Calculate final velocities based on pressure (see equation 3 and serial code)
- Transfer domain boundary final velocities to neighbours
- Increment time and repeat from step 1 if final time has not yet been reached
The code must be able to use an overall domain of arbitrary size so that you can test your simulator’s efficiency as the domain size is changed. You should also ideally be able to change the height and width of the domain independently of one another (how might this impact the best decomposition?).
You probably don’t want to do an output every time step as the time steps may be quite small, but rather at a user specified interval (ideally in terms of time rather than time steps). At these times you should write output to file. The most efficient method will probably be for each process to write their own files, though you could use MPI files to write to a single file. You should write a separate program or script which collates these files and generates a graphical output. This can be done in Python.
Performance Analysis
In addition to documented source code you should also submit a short report which includes an analysis of the performance of the code. I wish to see how the Efficiency/Speedup changes with the size of the problem and the number of cores used. You will need to use the HPC system if you are to test this on a suitable number of cores to see good trends. How does the efficiency behaviour compare to what you might have expected?
Because you can use a dynamic time step that depends on resolution, as well as having an internal iteration where the convergence could well depend on resolution, there are a number of different runtimes that you may need to consider - total simulation time, time per timestep, time per Jacobi iteration (including communication). Also remember that you will need to consider averages for these and will need to run the simulations multiple times to get robust results.
There are two submission deadlines for this coursework. The reason for this two stage submission is so that people are not working on this coursework during the group project. You will be given access to the HPC system once the group project is complete.
Submission
What is required to be in the GitHub repository
First submission deadline:
- Documented source code
- Both simulation and post-processing code
Second submission deadline:
- Both simulation and post-processing code
- Videos/animations of the simulation output
- Short report on the performance of the code
- The report has a 1000 word limit, but can be accompanied by figures
- Output log files from your HPC runs (.o files)
Mark Scheme
- Code commenting and documentation
- Code implementation, structure and efficiency
- Postprocessing code
- Results
- Analysis and discussion of the program’s performance
- Extensions and additional implementations
What is required in the code
In this assignment I want you to demonstrate your MPI programming skills. The code MUST therefore make use of the following MPI techniques:
Required:
- Non-blocking point to point communications
- Collective communications for determining the time step and residual
- Creating your own MPI variable types
- You MUST use MPI_Type_create_struct - There are other easier ways to make MPI data types for very structured data like this, but I want you to demonstrate that you know how to do generic MPI datatype creation
Optional
- Doing calculations while waiting for communications to complete - You will need to watch out to make sure that you are not doing calculations that require the data from the neighbouring processors while waiting
- Internal boundaries and obstacles for the fluid to interact with
- You can also create a SEPARATE/EXTRA version using one-sided communications - The main version associated with virtually all of the marks will be the version using Nonblocking point to point communications. Therefore only try and do the one-sided communications version if the other version is complete, working well, profiled, documented etc and you have spare time. This would be more for your own interest than it would be for the extra marks!
- Similarly to above, you could also try to create a SEPARATE/EXTRA version that uses a staggered grid to try and get around the problem of having instabilities in the pressure field. Note that this will be a challenge in terms of both having to derive the appropriate discretisations (though I am willing to check them) and the neighbouring communications pattern required.