使用改进的Backtracking搜索算法,完成Battleship游戏的部署。
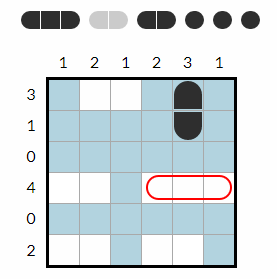
Introducing Battleship Solitaire
In this assignment, you will write a program to solve Battleship Solitaire puzzles. This will require you to encode these puzzles as a constraint satisfaction problem (CSP) and implement a CSP solver.
Battleship Solitaire is similar to the Battleship board game Links to an external site.. Unlike the 2-player board game, Battleship Solitaire shows the number of ship parts in each row and column, and your goal is to deduce the location of each ship.
You can play games of battleship solitaire for free at https://lukerissacher.com/battleships Links to an external site..
The rules of Battleship Solitaire are as follows.
- There are four types of ships.
- Submarines (1x1)
- Destroyers (1x2)
- Cruisers (1x3)
- Battleships (1x4)
- Each ship can be either horizontal or vertical, but not diagonal.
- (Ship constraints) The puzzle describes the number of each type of ship.
- (Row constraints) The number to the left of each row describes the number of ship parts in that row.
- (Column constraints) The number at the top of each column describes the number of ship parts in that column.
- Ships cannot touch each other, not even diagonally. In other words, each ship must be surrounded by at least one square of water on all sides and corners.
- Some puzzles also reveal the contents of certain squares, showing whether they contain water or a ship part.
- Where a ship part is revealed, it will indicate whether it is a middle or end portion of a ship. If the ship part is the end portion, it will show the part’s orientation.
- When a submarine (1x1) is revealed, it shows the entire ship.
Your Tasks
You will implement a program to solve Battleship Solitaire using backtracking search, forward checking, AC-3 arc consistency, or any other techniques you choose.
Running Your Program
You will submit a file named battle.py, which contains your program that solves a Battleship Solitaire puzzle.
Your program must use python3 and run on the teach.cs server (where we run our auto-testing script).
We will test your program using several Battleship Solitaire puzzles. For each puzzle, we will run the following command.
python3 battle.py --inputfile <input file> --outputfile <output file>
Each command specifies one plain-text input file and one plain-text output file.
For example, if we run the following command for an input file puzzle1.txt:
python3 battle.py --inputfile puzzle1.txt --outputfile solution1.txt
The solution to puzzle1.txt will be in solution1.txt.
Input Format
The input file has the following format.
- The first line describes the row constraints as a string of N numbers.
- The row constraints are usually written to the left or the right of each row when viewing examples of these puzzles.
- The second line describes the column constraints as a string of N numbers.
- The column constraints are usually written on the top or bottom of each column when viewing examples of these puzzles.
- The third line describes the number of each type of ship.
- The four numbers represent the number of submarines (1x1), destroyers (1x2), cruisers (1x3) and battleships (1x4) in that order.
- The remaining lines will be an NxN grid representing the initial layout of the puzzle. There are eight possible characters for each cell.
- ‘0’ (zero) represents no hint for that square.
- ‘S’ represents a submarine,
- ‘.’ (period) represents water.
- ‘<’ represents the left end of a horizontal ship,
- ‘>’ represents the right end of a horizontal ship,
- ‘^’ represents the top end of a vertical ship,
- ‘v’ (lower-cased letter v) represents the bottom end of a vertical ship.
- ‘M’ represents a middle segment of a ship (horizontal or vertical).
An example of an input file would be:
211222
140212
3210
000000
0000S0
000000
000000
00000.
000000
Output format
The output contains an NxN grid representing the solution to the puzzle. Each cell has 7 possible values. There should be no ‘0’ characters left in the output file. See the correct output for the earlier example below.
<>....
....S.
.^....
.M...S
.v.^..
...v.S
Submission
You should submit one file on MarkUs:
- battle.py has your Python program that solves a Battleship Solitaire puzzle.
We will test your program on several puzzles of various sizes. For each puzzle, your program must terminate within 4 minutes. We strongly recommend testing your program on the teach.cs server to ensure that it terminates within the time limit.
We will provide three puzzles to you on MarkUs. Please use these to test the correctness and efficiency of your program.
Starter Code
We have provided a considerable amount of starter code. We highly recommend taking lots of time to read the starter code and understand what it is doing.
- csp.py has a Variable class, a Constraint class, and a CSP class.
- constraints.py defines three Constraint classes: TableConstraint, NValuesConstraint, and IfAllThenOneConstraint.
Your main tasks are to:
- Create a CSP containing variables and constraints.
- Implement backtracking search and constraint propagation (forward checking or AC-3) to solve the CSP.
Suggestions
Formulating variables and constraints:
- Avoid variables that require an exponential number of values. Performing constraint propagation on such constraints will be too expensive.
- Avoid using table constraints over a large number of variables. Table constraints over two or three variables are fine: performing constraint propagation on table constraints with large numbers of variables becomes very expensive.
Backtracking and constraint propagation:
- Never perform plain backtracking. Consider using AC-3 instead of forward checking if you have some non-binary constraints.
- It may be challenging to deal with ship constraints using forward checking or AC-3. Here is our suggestion. Ignore the ship constraints first and find all the solutions that satisfy the other constraints. Then, iterate through all the solutions and find the solution that satisfies the ship constraints.
- For faster constraint propagation (forward checking or AC-3), try formulating constraints with fewer variables instead of more variables. Split as many higher-order constraints (involving many variables) into binary constraints as possible.
- There are binary constraints that might help propagation. For example, every square occupied by anything other than W or 0 must have each of its diagonals be W. So every pair of diagonal squares (x, y) on the board can have a constraint C(x, y): x == ‘W’ or y == ‘W.’
- Consider creating a lookup table for past arc consistency supports to save time when revisiting variables in the AC-3 algorithm.
- Preprocessing can help, especially if your constraint propagation implementation is inefficient. For example, you can pad certain squares with water before the search begins. Also, you know columns/rows that add up to 0 are all water.
Heuristics:
- To make your solution more efficient, consider implementing heuristics for choosing a variable or a value (e.g. Minimum-Remaining-Value heuristic, Degree heuristic, and Least-Constraining-Value heuristic)