根据提供的伪代码,用GA算法解决优化问题。
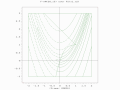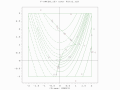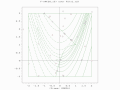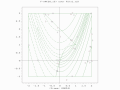
Goals
To implement a fully functional microbial GA or another optimisation algorithm.To investigate the effects of population size, mutation rate and recombination rate on evolution.
The problems is the same as last week. The knapsack (KP) problem is an example of a combinatorial optimization problem. It is concerned with a knapsack that has positive integer volume (or capacity) V . There are n distinct items that may potentially be placed in the knapsack. Item i has a positive integer volume Vi and positive integer benefit Bi . In the most basic form of the problem we will consider there are only one of each item available (0-1 KP).
The goal is to maximize value, subject to the constraint, resourceProblem.m for this weeks problem.
Either use a full optimisation algorithm of your choice on the above problem or follow the sheet below.
Task 1
Implement a steady state GA with tournament selection. You will need a population of N individuals. This should be encoded as a matrix of N genotypes, wherein each genotype encodes one possible solution to knapsack problem. A genotype phenotype mapping. A fitness function . We need a way to evaluate how good each phenotype is as a potential solution to the card-sorting problem. A tournament selection method a mutation operator.
Pseudocode is as follows:
- Initialise random pop P
- Pick 2 individuals at random & evaluate them finding a winner (W) and loser (L)
- Copy W over L and add a mutation to the loser
- Until success or give up, goto 2
(Remember that N evaluations of this sort is equivalent to a generation in traditional GA)
How well does it perform. Does it do better than the hillclimber from last week? Whats is the effect of the mutation rate?
Task 2
Implement a spatial GA. You will to put the population of N individuals on 1D array .
Pseudocode is as follows:
- Initialise random pop P
- Associate each individual with a position x, i.e, let the position of the genotype in the population array indicate the position on a 1D grid.
- Pick one individual at random, i.e. genotype G1 at position x1
- Pick a second individual G2 in the local neighbourhood of the first, i.e., pick a competitor from the local neighbourhood in the range x1 to x1+k. Or see code in lecture for simpler implementation
- Compare G1 and G2 finding a winner (W) and loser (L)
- Copy W over L and add a mutation (remember to reevaluate the fitness of the loser)
- Until success or give up, goto 3
How do this algorithm compare to the first. Does it evolve quicker? Does it get stuck in local minima more or less often?
Task 3
Construct a full microbial GA. To do this you will need a recombination operator , see Lectures for full code. Pseudo code is as follows.
Pseudocode is as follows:
- Initialise random pop P
- Associate each individual with a position x, i.e, let the position of the genotype in the population matrix indicate the position on a 1D grid.
- Pick one individual at random, i.e. genotype G1 at position x1
- Pick a second individual G2 in the local neighbourhood of the first, i.e., pick a competitor from the local neighbourhood in the range x1-k ro x1+k (start with k=2)
- Compare G1 and G2 finding a winner (W) and loser (L)
- Copy each gene of the winner W to the L with crossover probability (Pcrossover, say 0.5 to start)
- Add a mutation to the L (remember to reevaluate the fitness of the loser)
- Until success or give up, goto 3
How does this algorithm compare to the first two? Does it evolve quicker? Does it get stuck in local minima more or less often. What is the effect of Pcrossover on the speed of evolution